These are two problems I’ve worked on from my Artificial Intelligence class this semester. These are problems which can take a really long time if done naively, hence the goal is to come up with solutions that use some heuristic to come up with the answer faster.
Snake-in-the-box
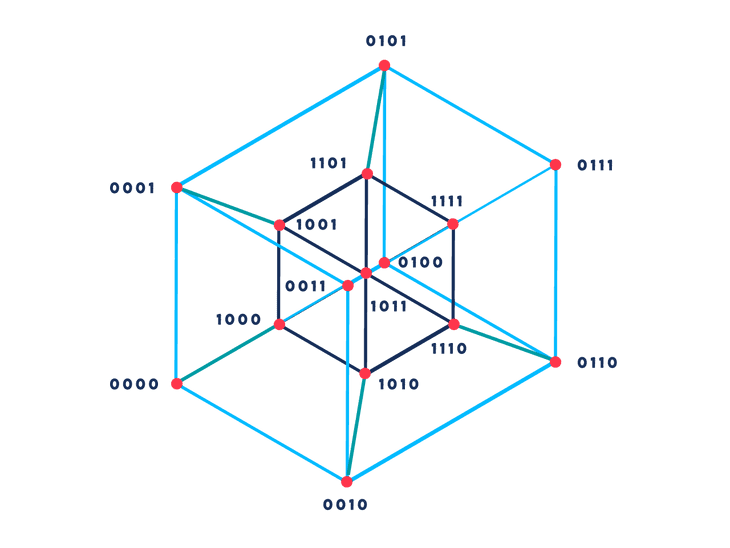
The Snake-in-the-box problem begins with a n dimensional hypercube. It consists of finding a path (the “snake”) in this cube, in which every node has exactly two neighbors that are also in the path. The only exception is the head and tail, which can be connected to each other in other to create a continuous path.
Example 4-dimensional hypercube:
A nice property about each node in a n-dimension cube is that they can be represented in n-digit binary numbers, and the difference between neighbors is one bit flip (In a 4-dimension hypercube, 0000 and 0001 are neighbors).
This property allows us to easily compute the neighbors of each node, regardless of the dimension of the cube, which means that if we write a program to compute the solution we don’t necessarily have to compute and store every node in the cube.
While computing a 3 or 4 dimensional hypercube is very trivial, as we move up to higher dimensions, the space needed grows exponentially.
A almost-naive solution
The following is an almost-naive (a.k.a partially brute-force) solution to this problem. It takes advantage of the bit-flip property, but it lacks any other heuristic or optimization.
The problem with this implementation lies on the fact that it still has to do a full search.
It’s written in PHP, and it’s very object-oriented, so it’s not super fast, but it does get the correct solution if you let it run for long enough:
https://github.com/eduard44/snakes
So far I’ve been able to get solutions for dimensions 3 to 6: 4, 7, 13, 26. Dimension 6 took a really long time to process on my cheap VPS, so I’m not expecting dimension 7 to finish any time soon.
Possible future steps are: Rewrite the whole thing in a more efficient language like C++ or implement some heuristic or algorithm that accelerates the execution runtime.
Sample output
$ hhvm run.php snakes -d 3
> Largest path found was: 4
$ hhvm run.php snakes -d 4
> Largest path found was: 7Update 1: Randomized version
Another approach to this problem is to randomly select the path every time. This means that the search algorithm can return anywhere between the actual longest snake and 1.
To compensate for this, we can run the algorithm for multiple iterations, and keep track of the longest result.
This does not necessarily yield the correct solution, but it allows us to take a look at paths that at least get closer to the longest solution on higher dimensions.
As a nice added extra, I was able to use a Symfony component for displaying information about the progress of the program, including an estimate of how much time it will take to go through all the iterations:
Find the zebra
The find the zebra problem is much simpler. It consists of a group of five houses, which are next to each other in a neighborhood. Each house has 5 properties:
- A color
- The nationality of the owner
- A pet/animal
- The favorite drink of the owner
- The favorite cigar/smoke brand of the owner (It’s an old problem, on 2014 you could replace it with something like favorite smartphone brand)
To find the solution, you must derivate rules from other rules recursively. The rules provided are (via Wikipedia):
- There are five houses
- The Englishman lives in the red house
- The Spaniard owns the dog
- Coffee is drunk in the green house
- The Ukrainian drinks tea
- The green house is immediately to the right of the ivory house
- The Old Gold smoker owns snails
- Kools are smoked in the yellow house
- Milk is drunk in the middle house
- The Norwegian lives in the first house
- The man who smokes Chesterfields lives in the house next to the man with the fox
- Kools are smoked in the house next to the house where the horse is kept
- The Lucky Strike smoker drinks orange juice
- The Japanese smokes Parliaments
- The Norwegian lives next to the blue house
The two questions asked are: Who drinks water? and who owns the zebra?
Solution by elimination
To approach I took to this problem, revolves around coming up with all possible permutations and eliminating possible solutions by applying each rule one by one.
How do we represent the problem?
I chose to store the problem in a two-dimensional array (a matrix), in which each row is a category and each column is a house. This means that we have a matrix of 5 x 5.
On each row, we have 5! = 120 possible permutations (Permutation formula). On the whole table, we have (5!) * 5 = 600 possible arrangements.
It is simple to compute each of these arrangements and store them in memory, but individually checking that they meet the ruleset might take a really long time.
Reducing the initial size
The good news is that we don’t have to check every single arrangement. How? You may have noticed that three of the rules above are marked in bold. These rules are special because they are the only rules that give us a hint on where to start. From them we know that:
- The Norwegian lives in the first house
- The blue house is the second house
- Milk is drank in the third (middle) house
So, when we are generating our array of all possible combinations, we can safely discard combinations that do not meet these conditions, greatly reducing our search space.
Applying rules
For all the other rules, we apply a similar strategy. We take the array of possible combinations, check which combinations match the rule and discard those that don’t. At the end, every rule we apply, reduces the size of the search to a smaller subset, meaning that each subsequent rule will execute faster. This will lead to better execution time than if we checked each combination individually against all rules.
The code:
I used NodeJS (JavaScript) to implement this solution, which ran pretty fast (about 1-2 mins, depending on the CPU). At the end, it actually found two solutions!
Please note that some of the nouns might be different from the rules above since our class used a different problem, but it’s essentially the same ruleset.
You can check the code here:
https://github.com/etcinit/ai-zebra1
Sample output
$ node zebra.js
[{
nationalities:
[ 'Norwegian', 'Ukrainian', 'Englishman', 'Spaniard', 'Japanese' ],
colors: [ 'Yellow', 'Blue', 'Red', 'White', 'Green' ],
drinks: [ 'Water', 'Tea', 'Milk', 'Juice', 'Coffee' ],
pets: [ 'Fox', 'Horse', 'Serpent', 'Dog', 'Zebra' ],
smokes:
[ 'Kool', 'Chesterfield', 'Winston', 'Lucky Strike', 'Kent' ]
}, {
nationalities:
[ 'Norwegian', 'Ukrainian', 'Englishman', 'Japanese', 'Spaniard' ],
colors: [ 'Yellow', 'Blue', 'Red', 'Green', 'White' ],
drinks: [ 'Water', 'Tea', 'Milk', 'Coffee', 'Juice' ],
pets: [ 'Fox', 'Horse', 'Serpent', 'Zebra', 'Dog' ],
smokes:
[ 'Kool', 'Chesterfield', 'Winston', 'Kent', 'Lucky Strike' ]
}]